Khi nói đếnăng-tenCâu hỏi mà mọi người quan tâm nhất là "Bức xạ thực sự được tạo ra như thế nào?" Làm thế nào trường điện từ do nguồn tín hiệu tạo ra lan truyền qua đường truyền và bên trong anten, và cuối cùng "tách" ra khỏi anten để tạo thành sóng trong không gian tự do?
1. Bức xạ dây đơn
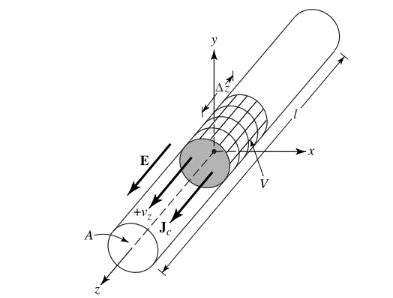
Giả sử mật độ điện tích, được biểu thị bằng qv (Coulomb/m3), được phân bố đều trong một dây dẫn hình tròn có diện tích mặt cắt ngang là a và thể tích là V, như thể hiện trong Hình 1.
Hình 1
Tổng điện tích Q trong thể tích V chuyển động theo hướng z với tốc độ đều Vz (m/s). Có thể chứng minh rằng mật độ dòng điện Jz trên tiết diện ngang của dây dẫn là:
Jz = qv vz (1)
Nếu dây dẫn được làm từ chất dẫn điện lý tưởng, mật độ dòng điện Js trên bề mặt dây dẫn là:
Js = qs vz (2)
Trong đó qs là mật độ điện tích bề mặt. Nếu dây dẫn rất mỏng (lý tưởng là bán kính bằng 0), dòng điện trong dây dẫn có thể được biểu diễn như sau:
Iz = ql vz (3)
Trong đó ql (coulomb/mét) là điện tích trên một đơn vị chiều dài.
Chúng tôi chủ yếu quan tâm đến dây dẫn mỏng và các kết luận áp dụng cho ba trường hợp trên. Nếu dòng điện thay đổi theo thời gian, đạo hàm của công thức (3) theo thời gian như sau:
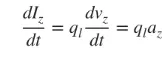
(4)
az là gia tốc điện tích. Nếu chiều dài dây là l, (4) có thể được viết như sau:
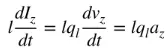
(5)
Phương trình (5) là mối quan hệ cơ bản giữa dòng điện và điện tích, và cũng là mối quan hệ cơ bản của bức xạ điện từ. Nói một cách đơn giản, để tạo ra bức xạ, phải có dòng điện biến thiên theo thời gian hoặc gia tốc (hoặc giảm tốc) của điện tích. Chúng ta thường đề cập đến dòng điện trong các ứng dụng điều hòa theo thời gian, và điện tích thường được đề cập trong các ứng dụng thoáng qua. Để tạo ra gia tốc (hoặc giảm tốc) của điện tích, dây dẫn phải bị uốn cong, gấp lại và không liên tục. Khi điện tích dao động theo chuyển động điều hòa theo thời gian, nó cũng sẽ tạo ra gia tốc (hoặc giảm tốc) điện tích tuần hoàn hoặc dòng điện biến thiên theo thời gian. Do đó:
1) Nếu điện tích không di chuyển, sẽ không có dòng điện và không có bức xạ.
2) Nếu điện tích chuyển động với vận tốc không đổi:
a. Nếu dây dẫn thẳng và có chiều dài vô hạn, sẽ không có bức xạ.
b. Nếu dây dẫn bị uốn cong, gấp lại hoặc bị gián đoạn, như thể hiện trong Hình 2, thì sẽ có bức xạ.
3) Nếu điện tích dao động theo thời gian, điện tích sẽ bức xạ ngay cả khi dây dẫn thẳng.
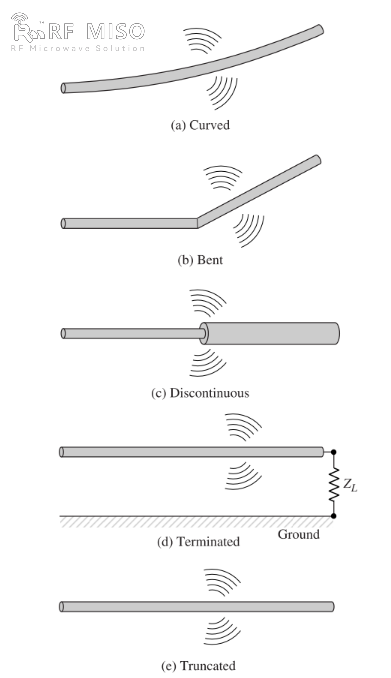
Hình 2
Có thể hiểu một cách định tính về cơ chế bức xạ bằng cách xem xét một nguồn xung được nối với một dây dẫn hở có thể được nối đất thông qua một tải ở đầu hở của nó, như thể hiện trong Hình 2(d). Khi dây dẫn được cấp điện ban đầu, các điện tích (electron tự do) trong dây dẫn được đặt vào chuyển động bởi các đường sức điện trường do nguồn tạo ra. Khi các điện tích được gia tốc ở đầu dây dẫn gần nguồn và bị giảm tốc (gia tốc âm so với chuyển động ban đầu) khi phản xạ ở đầu kia, một trường bức xạ được tạo ra ở các đầu dây và dọc theo phần còn lại của dây dẫn. Sự gia tốc của các điện tích được thực hiện bởi một nguồn lực bên ngoài đặt các điện tích vào chuyển động và tạo ra trường bức xạ liên quan. Sự giảm tốc của các điện tích ở các đầu dây dẫn được thực hiện bởi các lực nội tại liên quan đến trường cảm ứng, gây ra bởi sự tích tụ các điện tích tập trung ở các đầu dây dẫn. Các lực nội tại thu được năng lượng từ sự tích tụ điện tích khi vận tốc của nó giảm xuống bằng không ở các đầu dây dẫn. Do đó, sự gia tốc của các điện tích do kích thích điện trường và sự giảm tốc của các điện tích do sự gián đoạn hoặc đường cong trơn tru của trở kháng dây dẫn là các cơ chế tạo ra bức xạ điện từ. Mặc dù cả mật độ dòng điện (Jc) và mật độ điện tích (qv) đều là các số hạng nguồn trong phương trình Maxwell, điện tích được coi là một đại lượng cơ bản hơn, đặc biệt đối với các trường biến đổi theo thời gian. Mặc dù lời giải thích về bức xạ này chủ yếu được sử dụng cho các trạng thái biến đổi theo thời gian, nó cũng có thể được sử dụng để giải thích bức xạ ở trạng thái ổn định.
Tôi xin giới thiệu một vài gợi ý tuyệt vời.sản phẩm antenđược sản xuất bởiRFMISO:
2. Bức xạ hai dây
Nối nguồn điện áp với đường dây truyền tải hai dây dẫn được nối với ăng-ten, như thể hiện trong Hình 3(a). Việc đặt điện áp vào đường dây hai dây dẫn tạo ra một điện trường giữa các dây dẫn. Các đường sức điện trường tác động lên các electron tự do (dễ dàng tách ra khỏi nguyên tử) được nối với mỗi dây dẫn và buộc chúng phải chuyển động. Sự chuyển động của các điện tích tạo ra dòng điện, từ đó tạo ra một từ trường.
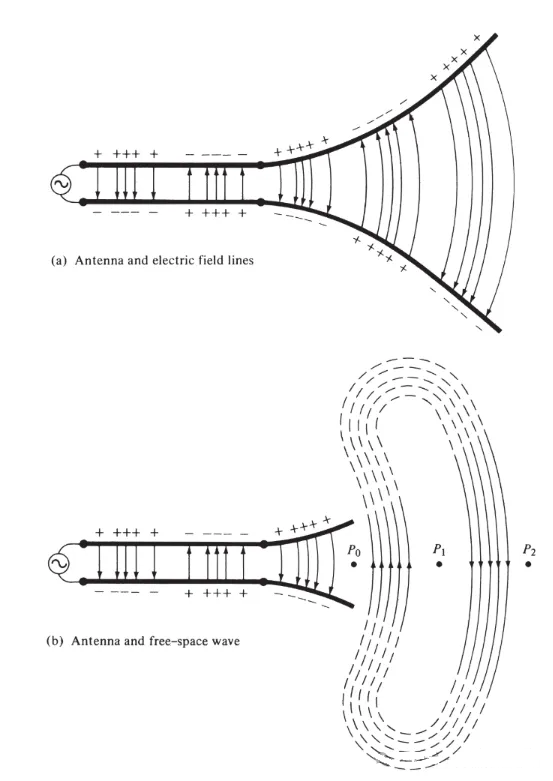
Hình 3
Chúng ta đã chấp nhận rằng các đường sức điện trường bắt đầu bằng điện tích dương và kết thúc bằng điện tích âm. Tất nhiên, chúng cũng có thể bắt đầu bằng điện tích dương và kết thúc ở vô cực; hoặc bắt đầu ở vô cực và kết thúc bằng điện tích âm; hoặc tạo thành các vòng kín không bắt đầu cũng không kết thúc bằng bất kỳ điện tích nào. Các đường sức từ luôn tạo thành các vòng kín xung quanh các dây dẫn mang dòng điện vì trong vật lý không có điện tích từ. Trong một số công thức toán học, các điện tích từ tương đương và dòng điện từ được đưa ra để thể hiện tính lưỡng nguyên giữa các nghiệm liên quan đến nguồn điện và nguồn từ.
Các đường sức điện trường vẽ giữa hai dây dẫn giúp thể hiện sự phân bố điện tích. Nếu giả sử nguồn điện áp là hình sin, ta kỳ vọng điện trường giữa các dây dẫn cũng là hình sin với chu kỳ bằng chu kỳ của nguồn. Độ lớn tương đối của cường độ điện trường được biểu thị bằng mật độ các đường sức điện trường, và các mũi tên chỉ hướng tương đối (dương hoặc âm). Sự tạo ra điện trường và từ trường biến thiên theo thời gian giữa các dây dẫn tạo thành một sóng điện từ lan truyền dọc theo đường truyền, như thể hiện trong Hình 3(a). Sóng điện từ đi vào anten cùng với điện tích và dòng điện tương ứng. Nếu ta loại bỏ một phần cấu trúc anten, như thể hiện trong Hình 3(b), một sóng không gian tự do có thể được hình thành bằng cách "nối" các đầu hở của các đường sức điện trường (được thể hiện bằng các đường chấm). Sóng không gian tự do cũng có tính tuần hoàn, nhưng điểm pha không đổi P0 di chuyển ra ngoài với tốc độ ánh sáng và đi được một khoảng cách λ/2 (đến P1) trong nửa chu kỳ thời gian. Gần ăng-ten, điểm pha không đổi P0 di chuyển nhanh hơn tốc độ ánh sáng và tiến gần đến tốc độ ánh sáng tại các điểm cách xa ăng-ten. Hình 4 thể hiện sự phân bố điện trường trong không gian tự do của ăng-ten λ/2 tại các thời điểm t = 0, t/8, t/4 và 3T/8.
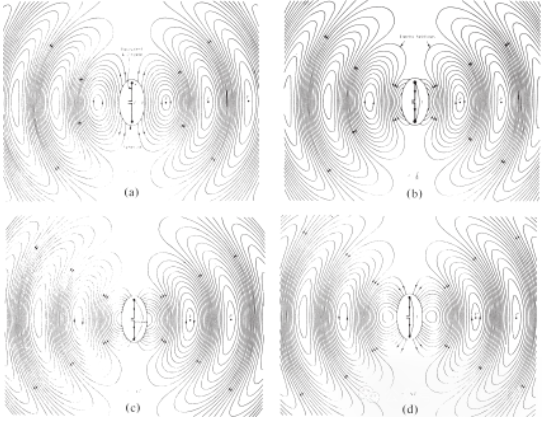
Hình 4. Phân bố điện trường trong không gian tự do của anten λ/2 tại các thời điểm t = 0, t/8, t/4 và 3T/8.
Hiện chưa rõ làm thế nào các sóng dẫn hướng được tách ra khỏi ăng-ten và cuối cùng hình thành để lan truyền trong không gian tự do. Chúng ta có thể so sánh sóng dẫn hướng và sóng trong không gian tự do với sóng nước, có thể được tạo ra bởi một hòn đá rơi xuống mặt nước tĩnh lặng hoặc bằng những cách khác. Khi sự nhiễu loạn trong nước bắt đầu, sóng nước được tạo ra và bắt đầu lan truyền ra ngoài. Ngay cả khi sự nhiễu loạn dừng lại, sóng vẫn không ngừng mà tiếp tục lan truyền về phía trước. Nếu sự nhiễu loạn kéo dài, các sóng mới liên tục được tạo ra, và sự lan truyền của những sóng này sẽ chậm hơn so với các sóng khác.
Điều tương tự cũng đúng với sóng điện từ được tạo ra bởi nhiễu loạn điện. Nếu nhiễu loạn điện ban đầu từ nguồn có thời gian ngắn, sóng điện từ được tạo ra sẽ lan truyền bên trong đường dây truyền tải, sau đó đi vào anten, và cuối cùng bức xạ ra ngoài không gian tự do, ngay cả khi sự kích thích không còn nữa (giống như sóng nước và nhiễu loạn mà chúng tạo ra). Nếu nhiễu loạn điện liên tục, sóng điện từ sẽ tồn tại liên tục và bám sát theo sau trong quá trình lan truyền, như được thể hiện trong anten hình nón đôi ở Hình 5. Khi sóng điện từ nằm bên trong đường dây truyền tải và anten, sự tồn tại của chúng có liên quan đến sự tồn tại của điện tích bên trong dây dẫn. Tuy nhiên, khi sóng được bức xạ, chúng tạo thành một vòng kín và không có điện tích nào để duy trì sự tồn tại của chúng. Điều này dẫn chúng ta đến kết luận rằng:
Việc kích thích từ trường đòi hỏi sự gia tốc và giảm tốc của điện tích, nhưng việc duy trì từ trường thì không cần sự gia tốc và giảm tốc của điện tích.
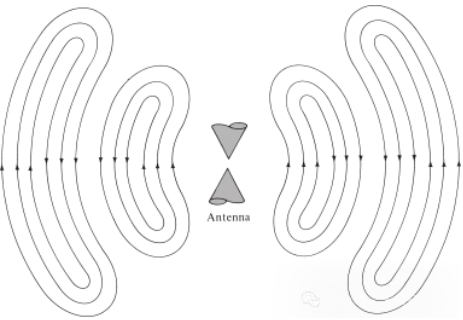
Hình 5
3. Bức xạ lưỡng cực
Chúng tôi cố gắng giải thích cơ chế mà các đường sức điện trường tách ra khỏi anten và tạo thành sóng trong không gian tự do, và lấy anten lưỡng cực làm ví dụ. Mặc dù đây là một giải thích đơn giản, nhưng nó cũng giúp mọi người hình dung trực quan sự hình thành sóng trong không gian tự do. Hình 6(a) cho thấy các đường sức điện trường được tạo ra giữa hai nhánh của lưỡng cực khi các đường sức điện trường di chuyển ra ngoài một khoảng λ/4 trong một phần tư chu kỳ đầu tiên. Trong ví dụ này, giả sử số lượng đường sức điện trường được hình thành là 3. Trong một phần tư chu kỳ tiếp theo, ba đường sức điện trường ban đầu di chuyển thêm một khoảng λ/4 nữa (tổng cộng λ/2 so với điểm xuất phát), và mật độ điện tích trên dây dẫn bắt đầu giảm. Có thể coi đây là sự hình thành do sự xuất hiện của các điện tích trái dấu, triệt tiêu các điện tích trên dây dẫn ở cuối nửa chu kỳ đầu tiên. Các đường sức điện trường được tạo ra bởi các điện tích trái dấu là 3 và di chuyển một khoảng cách λ/4, được biểu diễn bằng các đường chấm chấm trong Hình 6(b).
Kết quả cuối cùng là có ba đường sức điện trường hướng xuống trong khoảng cách λ/4 đầu tiên và cùng số lượng đường sức điện trường hướng lên trong khoảng cách λ/4 thứ hai. Vì không có điện tích tổng cộng trên anten, các đường sức điện trường phải bị buộc phải tách ra khỏi vật dẫn và kết hợp lại với nhau để tạo thành một vòng kín. Điều này được thể hiện trong Hình 6(c). Trong nửa sau, quá trình vật lý tương tự được diễn ra, nhưng lưu ý rằng hướng ngược lại. Sau đó, quá trình được lặp lại và tiếp tục vô thời hạn, tạo thành một phân bố điện trường tương tự như Hình 4.
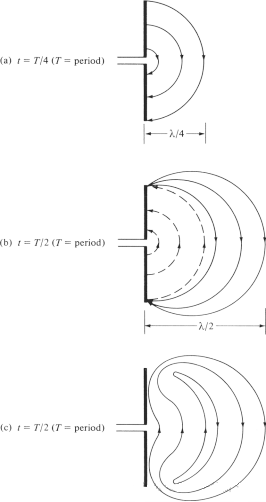
Hình 6
Để tìm hiểu thêm về ăng-ten, vui lòng truy cập:
Thời gian đăng bài: 20/06/2024










